Month: July 2014

I Miss Mitt (America Does, Too)

by

I’ve been saving this adorable BuzzFeed Politics article since I saw it a couple of weeks ago: Mitt Romney Has The Same Problems We All Have Flying Coach. It made me miss Mitt–by which I mean, miss what might have been–almost as much as the documentary Mitt.

2014-07-30 Mitt's Pink iPad
There are lots of photos of him flying coach, but my favorite is the one with the pink iPad.

Then today I saw this article in The Week: Americans really wish they had elected Mitt Romney instead of Obama.

Americans are so down on President Obama at the moment that, if they could do the 2012 election all over again, they’d overwhelmingly back the former Massachusetts governor’s bid. That’s just one finding in a brutal CNN poll, released Sunday, which shows Romney topping Obama in a re-election rematch by a whopping nine-point margin, 53 percent to 44 percent. That’s an even larger spread than CNN found in November, when a survey had Romney winning a redo 49 percent to 45 percent.

Yes, as the article says, you should take the polls “with a grain of salt,” but at the same time the list of things Romney was right about is both extensive and depressing.[ref]BuzzFeed again, humorously.[/ref]

Well, we’ll never know what could have been. But hey, maybe in 2016 we’ll get a chance at the next best thing. It’s not likely–and I’m not sure it’s politically wise–but I’m still hoping.

Ivy for Me, But Not for Thee: The Real Reason To Shun Elite Education

by
Image from Questier.com, where apparently they like to break the rules.
Image from Questier.com, where apparently they like to break the rules. (Note sign in bottom left.)

William Deresiewicz’s article for The New Republic Don’t Send Your Kid to the Ivy League definitely rubbed me the wrong way, and it didn’t take long to put my finger on it. From Deresiewicz’s Wikipedia page:

Deresiewicz attended Columbia University, where he majored in biology-psychology and graduated in 1985. He received a Masters in journalism from the same school in 1987 and a Ph.D. in English in 1998.

Not that Deresiewicz was hiding his Ivy League creds in the article itself. He wrote:

It was only after 24 years in the Ivy League—college and a Ph.D. at Columbia, ten years on the faculty at Yale—that I started to think about what this system does to kids and how they can escape from it, what it does to our society and how we can dismantle it.

See, it’s not so much that his Wikipedia entry gives away some big secret that he went to an Ivy League school. Nope, the point is that he has a Wikipedia page. So right off the bat, we’re not talking about some Joe on the street. We’re talking a notable person. For someone to spend a quarter century in the Ivy League and then (after they have become a notable person) to decide that it’s a terrible, terrible stifling place after all is a little bit rich. Consider also the fact that Deresiewicz’s primary complaints about the Ivy League are the kind of complaints that only a person without real, pressing, economic concerns can have.

“Return on investment”: that’s the phrase you often hear today when people talk about college. What no one seems to ask is what the “return” is supposed to be. Is it just about earning more money? Is the only purpose of an education to enable you to get a job? What, in short, is college for?

Deresiewicz answers: “The first thing that college is for is to teach you to think.” It’s all well and good for successful academics to talk about the supreme importance of the life of the mind. After all, that’s what they are paid to do, right? But not everyone is so lucky.

I love the life of the mind. If I won the lottery I would spend the rest of my life in college, earning degrees in one field after another. Math, physics, history, languages, linguistics, architecture, medicine, computer science: there’s almost nothing I wouldn’t love to spend a lifetime studying. But the fact is I haven’t won the lottery, and a great deal of my life therefore revolves around the struggle to keep from having to move my wife and children back into my parents house for a second time.

Those of us who aren’t looking backwards from the comfort of a secure and prosperous career, but are rather looking forward at the daunting prospect of navigating these troubled economic times with solvent households are very concerned with “return on investment.” But it’s not because we’re unenlightened barbarians with no appreciation for the life of the mind. It’s because bills don’t pay themselves. Has Deresiewicz forgotten that? Or did he simply never know?

I will give him credit for this, however: his excoriation of elite schools as propagators of social injustice is an argument that does ring true to me. I have never seriously considered that Yale or Harvard could give me or my kids a better education than a good state school. The point of elite education is not to learn more. It’s get access to a better network and a better brand. My concern about sending my kids to the Ivies (should that be a possibility) has always queasiness at the trade off between encouraging them to participate in morally noxious elitism vs. wanting them to have an easier time of it than I have.[ref]I wouldn’t feel bad if it was meritocratic, but it’s not.[/ref]

I also have to give him credit for having an appropriately expansive definition of “elite education”:

When I speak of elite education, I mean prestigious institutions like Harvard or Stanford or Williams as well as the larger universe of second-tier selective schools, but I also mean everything that leads up to and away from them—the private and affluent public high schools; the ever-growing industry of tutors and consultants and test-prep courses; the admissions process itself, squatting like a dragon at the entrance to adulthood; the brand-name graduate schools and employment opportunities that come after the B.A.; and the parents and communities, largely upper-middle class, who push their children into the maw of this machine. In short, our entire system of elite education.

It’s not attendance at an Ivy that will turn your kid into a zombie. It’s the way parents must structure every aspect of their kids’ childhood (so called) in order to gain admittance into said school that does the damage. By the time the kids arrive, I’d argue they are about as zombified as can be.

But, it turns out, there is hope! Deresiewicz presumes–and so had I–that elite education has a significant monetary advantage. In researching this post, however, I learned that that assumption is not true at all. Alan Krueger at Princeton University and Stacy Dale at Mathematica Policy Research conducted a very clever study where they compared the earnings of kids who went to Ivy Leagues with kids who were accepted to the Ivy Leagues but opted to go to less-prestigious universities. Since both groups got in, arguably both groups are roughly commensurate in terms of ability. So if the Ivy Leagues really have a return on investment (whether its from better education, better networking, or any other factor at all) the cohort that attended should have gotten higher earnings. But they didn’t. The two groups–those who attended Ivy League schools and those who were accepted did not–earned the same over the next decades (the original cohort started school in 1976, but the findings hold for a new cohort that entered in 1989).

That, for me, is a real reason not to send your kids to the Ivies. It’s not that some intellectual who has reaped the rewards of elite education for decades patronizingly tells you to “do as I say, not as I did.” It’s because they probably aren’t worth it in most cases. There are probably exceptions, like going to Yale Law if you want to teach law, that might apply at the very top of certain fields, and data also suggests that poor kids have the most to benefit from elite education, but in general (and especially for undergrad) it looks like your kids will be better off, all things considered, going to a good state school. And hey, they might get a real childhood that way, too.

The Dark Side of Emotional Intelligence is Obvious

by

2014-07-28 Emotional Intelligence

I came across an Atlantice article (from back in January) called The Dark Side of Emotional Intelligence. The article itself is rather boring. It is full of non-insights such as the fact that people who are highly emotionally intelligent (e.g. good at regulating their own emotions and intuiting the emotions of others) can be exceptional manipulators.[ref]In other ground-breaking research, social scientists discover that people who are very big and physical strong can beat up people who are smaller and weaker. And sometimes do.[/ref] It’s totally obvious that emotional intelligence would be a benefit in sectors like sales and customer service, and perhaps just mildly interesting that it would actually be a hindrance for mechanics and accountants. All of this leads to a completely banal concluding paragraph:

Thanks to more rigorous research methods, there is growing recognition that emotional intelligence—like any skill—can be used for good or evil. So if we’re going to teach emotional intelligence in schools and develop it at work, we need to consider the values that go along with it and where it’s actually useful. As Professor Kilduff and colleagues put it, it is high time that emotional intelligence is “pried away from its association with desirable moral qualities.”

The one thing that did strike my interest–and the reason I’m blogging about this–is the incredibly peculiar notion that The Atlantic thought there was anything at all to report here. Do we really live in a society where people associate emotional intelligence (which is basically just one particular form of power) with virtue? And, if so, where on earth did the notion come from?

I’m not quite willing to go so far as to say that the opposite is more intuitive–that emotionally (or otherwise) intelligent folks ought to be less moral–but it would at least certainly fit the age-old wisdom that power is fundamentally corrosive.

 

Immigration and the Poor

by
Pretty much
Pretty much. The claims provoking this sign tend to be untrue.

Immigration is in the news again with the influx of Central American children across U.S. borders. Some of the responses to these child immigrants have shown the ugly side of American nationalism. This skepticism toward immigration can be traced back to several of the Founding Fathers, including Benjamin Franklin, Thomas Jefferson, Alexander Hamilton, George Washington, and John Jay.[ref]Historian Thomas E. Woods, Jr. discusses their various concerns in his 33 Questions About American History You’re Not Supposed to Ask (New York: Three Rivers Press, 2007). However, some anti-immigration Americans assume immigrants are predominantly criminals, which the evidence doesn’t bear out. Furthermore, we often ignore how our own policies (such as the War on Drugs) helps create undesirable environments from which these immigrants want to escape.[/ref] However, even the skeptics among the Founders expressed the benefits of immigration. But I’m not particularly interested in cherry-picking Founders statements. What I am interested in is alleviating global poverty. Here are a few links that cover a variety of studies demonstrating increased immigration does just that:

  • Economist David Henderson, writing in a 2012 issue of The Freeman, notes, “Boston University economist Patricia Cortes, in a study published in the Journal of Political Economy, found that cities with larger influxes of low-skilled immigrants had lower prices for labor-intensive services such as dry cleaning, childcare, housework, and gardening. In a later study, Cortes and coauthor Jose Tessa found that these low-price services allowed Americans, especially women, to spend more hours working in high-skilled, high-paying jobs.The gains from eliminating barriers to immigration are huge. In a recent article in the Journal of Economic Perspectives, economist Michael Clemens finds that getting rid of all immigration restrictions worldwide would approximately double world GDP.” He continues, “…Harvard University economist Lant Pritchett’s observ[es] that the average gain from a lifetime of microcredit in Bangladesh, such as that provided by Nobel Peace Prize winner Mohammed Yunus’s Grameen Bank, is about the same as the gain from eight weeks working in the United States. Asks Pritchett, “If I get 3,000 Bangladeshi workers into the US, do I get the Nobel Peace Prize?” …Pritchett found that if rich countries allowed just a 3 percent increase in their labor forces through immigration, the world’s have-nots would benefit by $300 billion a year, and the residents of the rich countries would benefit by $51 billion a year.”
  • The Economist reports on a brand new study that “offer[s] ammunition for fans of more open borders. In 19 out of 20 countries, the authors calculated that shutting the doors entirely to foreign workers would make the native-born worse off. (Never mind what it would do to the immigrants themselves, who benefit far more than anyone else from being allowed to cross borders to find work.) The study also suggests that most countries could handle more immigration than they currently allow. In America, a one-percentage point increase in the proportion of immigrants in the population made the native-born 0.05% better off. The opposite was true in some countries with generous or ill-designed welfare states, however. A one-point rise in immigration made the native-born slightly worse off in Austria, Belgium, Germany, Luxembourg, the Netherlands, Sweden and Switzerland. In Belgium, immigrants who lose jobs can receive almost two-thirds of their most recent wage in state benefits, which must make the hunt for a new job less urgent. None of these effects was large, but the study undermines the claim that immigrants steal jobs from natives or drag down their wages.”[ref]This actually offers evidence for Milton Friedman’s initial point about immigration and the welfare state.[/ref]
  • Lydia DePillis at The Washington Post reports on two new papers that demonstrate immigrants fill labor gaps, complement existing capital, tech, and labor, and that this complementarity increases production and consequently wages.

Be sure to read and research the actual studies.

A Little on Hamas

by

The Israeli-Palestinian conflict is deeply personal to me. I am Israeli, and still have family in Israel. I also have Palestinian friends and acquaintances. Death and suffering are not abstract or theoretical notions. They will always affect someone that I know. As such, it can be a painful topic for me to discuss, but I do want to raise some perspectives that I feel are missing from the popular debates on blogs and social media now that violence has escalated in the Gaza Strip. Needless to say, my views are my own. Difficult Run has multiple voices, and welcomes different views. Before I proceed, I would like to direct the reader to two even-handed and reasonable pieces written by people that I know personally. While I disagree with both to some extent (the Mercurio quote can get tiresome), I appreciate the way that they frame their views, and recommend reading them. It is worth the time.

In this post I want to look at a major aspect of Hamas, the terrorist organization that became the ruling party in Gaza. Recently there have been several voices arguing that Hamas has been “horrendously misrepresented.” Most recently, Cata Charrett claimed that Hamas should be seen as a “pragmatic and flexible political actor.” This is essentially the same argument made earlier by others like Jeroen Gunning who produced pioneering research on the political side of Hamas.[ref]Gunning’s important study, Hamas in Politics, should be read cum grano salis due to an apologetic stance which spoils many of his insights. For example, Gunning considers that Hamas has “broadly followed” the ceasefire because although it fired rockets, it did not send suicide bombers.[/ref]

Hamas’ position, though, is not merely political, but draws deeply from certain metaphysical assumptions which frame their struggle. I’ll grant that divergent opinions certainly exist amongst the Hamas leadership. Some are pragmatists, and many others are decidedly hardliners. However, they do share a certain world-view.

Hamas’ founder, chief ideologue, and spiritual leader, Sheikh Ahmed Yassin, considered Palestine a waqf, that is, something consecrated to God. He formulated this belief as article 11 of Hamas’ Covenant, its charter document.

“The Islamic Resistance Movement believes that the land of Palestine is an Islamic waqf consecrated for future Muslim generations until Judgment Day. It, or any part of it, should not be squandered: it, or any part of it, should not be given up. Neither a single Arab country nor all Arab countries, neither any king or president, nor all the kings and presidents, neither any organization nor all of them, be they Palestinian or Arab, possess the right to do that. Palestine is an Islamic waqf land consecrated for Muslim generations until Judgment Day… This is the law governing the land of Palestine in the Islamic Sharia…”

Treating the land that way means that any permanent concessions can be construed as blasphemy against God himself and Islam (which of course aren’t considered completely separate concepts). There is also no earthly authority that can do so because it cannot speak for all Muslim generations. Compromise can only be tactical, and thus, limited. It makes negotiating with Hamas to achieve a peaceful state of coexistence a decidedly tricky prospect. As the concept is part of their founding covenant, it cannot simply be laid aside, even when they somewhat moderate their stance, or express some discomfort with the wording.[ref]The main discomfort has been more with the phrases used than the ideas behind them. This article discusses a Hamas initiative to change the Covenant’s wording, but eight years have passed with no change.[/ref] For example, much has been made of Hamas dropping the call to destroy Israel from its 2006 election manifesto. However, the evidence suggests that this was downplaying a fundamental position in order to focus on domestic political ambitions. The fundamental position itself did not change. This is despite Charrett’s insistence that the 1988 covenant is irrelevant to understanding the contemporary Hamas. Ghazi Hammad, a Hamas politician, said in 2006, that “Hamas is talking about the end of the occupation as the basis for a state, but at the same time Hamas is still not ready to recognise the right of Israel to exist… We cannot give up the right of the armed struggle because our territory is occupied in the West Bank and East Jerusalem. That is the territory we are fighting to liberate.”

Hamas has sought not a lasting peace, but a hudna, a temporary, multi-year cessation of violence for which it demands a very high price. Yes, Hamas has offered to recognize the June 1967 borders, but only for 10-20 years, and conditioned on Israel granting Palestinians the right of return and evacuating all settlements outside of said borders. Those terms should be worked out, but as part of a lasting, normative peace. When the twenty years are up (or less), Israel will find itself disadvantaged, its very existence considered an act of aggression. Khalid Mish’al, Hamas’ current leader, wrote in 2006 that, “We shall never recognise the right of any power to rob us of our land and deny us our national rights. We shall never recognise the legitimacy of a Zionist state created on our soil in order to atone for somebody else’s sins or solve somebody else’s problem.” In order to obtain another hudna, Israel will have to make concessions just as big. The possibility of permanent peace is vaguely left to the judgment of the next generation.[ref]While the conclusions of this paper are debatable, the quotes presented are very useful.[/ref]

Now, there are Jewish metaphysics of the land, too. The most famous is it being the land promised by God to his people Israel. Rabbi Yaakov Moshe Charlap, a prominent member of Rabbi Kook’s circle in the first half of the 20th century, considered the land of Israel a part of the highest aspect of the Divine. ‘‘In days to come, [the land of] Israel shall be revealed in its aspect of Infinity [Ein Sof], and shall soar higher and higher… Although this refers to the future, even now, in spiritual terms, it is expanding infinitely.’’ Charlap further considered Jewish settlement of the land of Israel as an essential condition for holiness to spread throughout the world. His teachings were very influential amongst radical Jewish settlers in the West Bank and the Gaza Strip. More recently, R. Yitzchak Ginsburg taught that Chabad’s seventh rebbe was the manifestation of the Divine, and that in order to return him to this world the land of Israel must be saved from “Arab hands.”[ref]Jonathan Garb, The Chosen will become Herds: Studies in Twentieth Century Kabbalah (Yale University Press, 2009), 62, 67-68.[/ref]

The major difference that I see is that Israel-even under a right-wing government- has shown itself willing to act against groups with such metaphysical views. When unilaterally disengaging from the Gaza Strip in 2005, the Israeli government dismantled the Jewish settlements, and expelled the settlers. The settler ideology (particularly in the Gaza Strip), as I’ve mentioned, was highly informed by teachings like that of Charlap’s. Such metaphysics, though, do not form an integral aspect of Israeli policy. Israel may be right or wrong about many things like the Gaza disengagement, but that is beside the point. Although I love it dearly, it is certainly an imperfect state. What matters here is the ability to lay aside metaphysics of the land and carry out concessions that are unpopular with many of its constituents.

Perhaps Hamas will change into a truly moderate force. Perhaps.

 

I Am An Object

by

2014-07-22 Jubal Early

Last week I was carrying my laptop out of my home office to use in another room and I tried to close the door behind me. I was, at the moment, deeply engrossed in some speculation that seemed very important to me at the time, which is I why I completely forgot about the pullup bar that had been hanging there for the last couple of weeks until it crashed down on my head.

I was indignant.

It didn’t really hurt much–and the laptop was unscathed–but it just didn’t seem befitting of my status as an agent which is to say an originator of actions. I make things happen. Things do not happen to me. “There is a God,” says the Book of Mormon, “and he hath created all things, both the heavens and the earth, and all things that in them are, both things to act and things to be acted upon.'[ref]2 Nephi 2:14[/ref] I know which of these I consider myself to be, as a general rule.

But we don’t always get to choose.

My frustration turned to amusement and I chuckled at myself. We think we are agents–and in a sense we are–but we’re also objects. We inhabit physical bodies that are subject to physical laws, and the laws of physics don’t give a whit for concepts like “narrative” or “justice” or “intention.” Because we live comfortable, safe live and are careful to avoid injuring ourselves, most of us manage to forget this most of the time. It takes a pretty horrific event (like a car crash) or a silly frustrating one (like closing a door and making a pullup bar drop on your head) to be reminded that we’re not exempt from the rules. Not even when we think we’re thinking very, very clever and deep thoughts.

Last week I dreamed of car crashes. Or, more specifically, I dreamed of that long endless moment between loss of control and impact. The period where you have just enough time to realize two things: that a collision is coming and that there’s nothing you can do about. The dream always started with a sudden lurch in the pit of my stomach and then the eery lack of sensation as the tires left contact with the road. Then a sense of weightlessness. I was always the passenger, not the driver, and I could never see out of the windshield of the car. I didn’t know how high we were, when we would hit, exactly what the car’s orientation was, or if I would survive. And even if I had known, there wasn’t anything I could do about it. Then a momentary flash of impact, and the dream restarted: the wheels no longer touching the road and me helplessly wondering what would come next.

That’s not always how life feels. But I think it’s probably what is always going on. We’re all Jubal Early at the end of the last Firefly episode “Objects in Space.” Adrift, we have freedom of movement, but nothing to push off of. We can flail in whatever way we would like during our indeterminate wait for death.

https://www.youtube.com/watch?v=VOhm-fS9Fa4

No, that’s not really how bleak my outlook on life is. But sometimes it feels that way.

Case Study: Winning the Argument Through Framing

by

2014-07-21 Explaining Conservatism

What explains conservatism? Famous left-leaning magazine MotherJones wants to know, and Chris Mooney writes about new research that might explain the puzzle in a piece that’s making the rounds on Facebook: Scientists Are Beginning to Figure Out Why Conservatives Are…Conservative. Here’s a part of the solution to the puzzle, right from the article:

The occasion of this revelation is a paper by John Hibbing of the University of Nebraska and his colleagues, arguing that political conservatives have a “negativity bias,” meaning that they are physiologically more attuned to negative (threatening, disgusting) stimuli in their environments. (The paper can be read for free here.) In the process, Hibbing et al. marshal a large body of evidence, including their own experiments using eye trackers and other devices to measure the involuntary responses of political partisans to different types of images. One finding? That conservatives respond much more rapidly to threatening and aversive stimuli (for instance, images of “a very large spider on the face of a frightened person, a dazed individual with a bloody face, and an open wound with maggots in it,” as one of their papers put it).

In other words, the conservative ideology, and especially one of its major facets—centered on a strong military, tough law enforcement, resistance to immigration, widespread availability of guns—would seem well tailored for an underlying, threat-oriented biology.

The reason I love this paper is because it’s not often that life hands me an example of prejudicial thinking so perfectly gift-wrapped for analysis. In this case, there’s absolutely no reason why the exact same underlying experimental evidence couldn’t be presented using a totally different frame. Instead of talking about a “negativity bias” and wondering why conservatives are so negative and speculating that this might explain conservatism, one could take the exact same data and talk about a “Pollyanna bias” and wonder why liberals are so unaware of threats and speculate that this might explain liberalism.

This is how political partisanship works, folks. It’s not that conservatives and liberals have different conclusions. Sure, that’s what most of the debates are about (for or against gun control, abortion, gay marriage, etc.) Those debates never get anywhere, however, because they miss the point. Conservatives and liberals see the world in different ways, and the way their conflicting world views actually compete with each other for followers is by spreading the assumptions that–if you accept them–lead logically to their policy positions. The way to win a debate is not by having more evidence or better reasoning because people don’t actually pay very much attention to evidence or reason. The way to win the debate–or at least to gin up your own side–is to frame it in such a way that you must be correct before the debate even starts.

Thus, in this case, Mooney starts out with the question: how do we explain conservatism? What he doesn’t actually come out and say–but what is actually the most important part of his piece–is the assumption that conservatism is an aberration and liberalism is the norm. There’s nothing about liberalism we have to explain; it’s just natural. But conservatism? It begs for some kind of explanation. Once you accept that premise, there’s really not much left to talk about. C. S. Lewis even invented a term for this debate style: bulverism:

The modern method [of argumentation] is to assume without discussion that [your opponent] is wrong and then distract his attention from this (the only real issue) by busily explaining how he became so silly. In the course of the last fifteen years I have found this vice so common that I have had to invent a name for it. I call it Bulverism. Some day I am going to write the biography of its imaginary inventor, Ezekiel Bulver, whose destiny was determined at the age of five when he heard his mother say to his father — who had been maintaining that two sides of a triangle were together greater than the third — ‘Oh you say that because you are a man.’ ‘At that moment’, E. Bulver assures us, ‘there flashed across my opening mind the great truth that refutation is no necessary part of argument. Assume that your opponent is wrong, and then explain his error, and the world will be at your feet. Attempt to prove that he is wrong or (worse still) try to find out whether he is wrong or right, and the national dynamism of our age will thrust you to the wall.’ That is how Bulver became one of the makers of the Twentieth [and Twenty-First] Century.[ref]C. S. Lewis, “Bulverism,” in God in the Dock, p. 273, which I got from here.[/ref]

As pleased as I am to have such a clear case study of Bulverism / winning the argument through framing ready at hand from now on, the thing that makes me sad is that it isn’t just MotherJones engaging in it. The researchers, by using the term “negativity bias” without an accompanying “positivity bias”, are jumping right in as well. (The name of their paper is: “Differences in negativity bias underlie variations in political ideology.”) Although sad, it’s hardly surprising. Dr. Jonathan Haidt was quoted about this very problem in the NYTimes back in 2011. Commenting on total domination of social psychology by the political left, he has said:

Anywhere in the world that social psychologists see women or minorities underrepresented by a factor of two or three, our minds jump to discrimination as the explanation. But when we find out that conservatives are underrepresented among us by a factor of more than 100, suddenly everyone finds it quite easy to generate alternate explanations.

The article goes on to quote him again:

Dr. Haidt argued that social psychologists are a “tribal-moral community” united by “sacred values” that hinder research and damage their credibility — and blind them to the hostile climate they’ve created for non-liberals.

It’s bad enough to have MotherJones serving up the Kool-Aid, but it’s really quite sad to have academic researchers as their direct suppliers.

As a coda: I do think that there are real and interesting psychological differences to study with regards to politics. But I think that this research is most useful when, as Haidt’s own Moral Foundations Theory does[ref]The book-length exposition of this theory in The Righteous Mind is one of the best non-fiction books I’ve ever read.[/ref], it seeks to take all sides seriously and create room for understanding and common ground. And not when, as with the articles in question, it serves as a flimsy excuse to pathologize your political opponents.

Pro-Russian Separatists Probably Shot Down the Malaysia Flight 17

by
2014-07-18 Malaysian Flight 17
Image Source, NYT

By now I’m sure everyone has heard about the Malaysian airliner that was shot down over Ukraine yesterday, killing nearly 300 people including over 20 Americans and about 100 HIV experts who were traveling to a conference in Australia. The plane was flying at an altitude (about 30,000 feet) that is outside the range of shoulder-fired surface-to-air-missiles, but within the range of mobile (truck-mounted) rockets. These kinds of rockets are in the hands of the Ukrainians, the Russians and–alarmingly–also pro-Russian separatists within Ukraine.

Lots of folks are saying we shouldn’t rush to judgment, and that’s usually the position I take, but in this case I think the evidence is already pretty clear. Within hours of the tragedy, NPR and others were reporting that a leader of the pro-Russian separatists had bragged on Twitter about downing a Ukrainian military transport plane at approximately the same time the Malaysian flight went missing. No such Ukrainian transport plane is missing, and the tweet was quickly deleted.

“In Torez An-26 was shot down, its crashes are lying somewhere near the coal mine “Progress,” read the tweet, obtained by FoxNews.com and translated into English. “We have warned everyone: do not fly in our skies.”

The self-titled “Self-defence forces of the Donetsk People’s Republic” boasted in a June 29 press release of having taken control of Buk missile defense systems. The Buk, or SA-11 missile launchers, have a range of up to 72,000 feet.[ref]Source[/ref]

The wreckage of plane came down in a separatist held region, and the black boxes are reportedly already shipped off to Moscow. It’s very unlikely that we will ever get really open, credible evidence because it is probably damning for Russia (since they gave the rocket launcher to the separatists). Meanwhile, the Ukrainians want to blame not only the separatists, but Moscow directly by alleging that it was Russian military forces (and not just their hardware on loan to rebels) that shot down the plane. It’s because we’re unlikely to get good information going forward that we may as well tentatively conclude what happened at this point.[ref]”We” in this case refers to folks just reading the newspapers like you and me. I hope that the experts, of course, conduct as thorough and objective an investigation as possible.[/ref]

The other reason it seems OK to call a tentative conclusion at this point is that the political ramifications are just not as important as people believe they are. ABC has a list of commercial airliners that have been shot down, and it includes the Ukrainians accidentally shooting down an airliner from Air Siberia in 2001, the infamous downing of Iranian flight 655 by the United States Navy guided missile cruiser USS Vincennes in 1988 and a Soviet fighter jet shooting down a Korean Air Lines plane in 1983.[ref]There are eight instances on the list altogether, going back to 1973.[/ref]

I don’t mean to diminish the tragedy at all. Quite the opposite. In some ways what is most tragic about this is that, from a geopolitical standpoint, it probably won’t really have much of an impact. If the Ukrainians, Russians, and Americans have all shot down passenger planes before on accident (and there’s no reason to suspect this wasn’t an accident as well) and World War III was averted, it’s unlikely major changes will come from this either. It might serve as a goad or a pretext for the EU to stiffen their stance somewhat in regards to Russia’s role in Urkaine, but it’s not going to change the fundamental nature of the conflict. The only real result, and I saw this with a sense of resignation, will be that airlines give up a little bit in their fuel-saving algorithms and re-route flights around the region.[ref]Airplane flight paths almost never look like what you expect them to, by the way, because we’re not very good at thinking about the world as a sphere. Look how far “north” the SF-Tokyo route goes, for example. That’s why I’ve got no idea what routes might usually fly through this region.[/ref]

One more note: part of why I think the first theory (that pro-Russian separatists shot down the plane when they thought it was a Ukrainian military transport) is that it’s so non-conspiratorial. There’s no great mystery, just a case of mistaken identification in a warzone. Something that, tragically, happens all the time. But if you do need any additional perspective on why a conspiracy is unlikely, read this: Count to ten when a plane goes down… It’s the first-hand account of how a 23-year old techie accidentally ignited decades of conspiracy theories after that Korean Air Lines jet was shot down in 1983 with a single mistaken keystroke.

Steep Learning Curve Doesn’t Mean What You Think It Does

by

Earlier this morning I read an article in The Verge about the resurgence of rogue-like games, which the author characterized with three core traits: “turn-based movement, procedurally generated worlds, and permanent death that forces you to start over from the beginning.” So far so good, but the author then added one additional, non-essential characteristic:

They also often have steep learning curves that force you to spend a lot of time getting killed before you understand how things actually work.

And that’s when I lost my mind.

“Steep learning curve” does not mean what Andrew Webster thinks it does. Yes, yes, I know: someone is wrong on the Internet. Egads! We can also bring up the usual academic description: should linguistics be descriptive (merely documenting how people talk) or should it be prescriptive (laying down grammatical rules and standardized definitions). In the long run, words  mean whatever people think they mean. Nothing more and nothing less. So I might be appalled by the fact that everyone uses “enormity” as though it meant “enormousness” these days[ref]It actually means “great evil,” or at least is used to.[/ref], but as a general rule I sigh, shake my head, and get on with my life.

The reality, of course, is that most of us understand grammar as a mixture of following the rules and knowing when to ignore or break them. The Week published a list of 7 bogus grammar ‘errors’ you don’t need to worry about, and their last category was “7. Don’t use words to mean what they’ve been widely used to mean for 50 years or more.” For example, the word “decimate” originally meant to kill 1/10th. It derives from a particularly brutal form of Roman military discipline[ref]”A cohort (roughly 480 soldiers) selected for punishment by decimation was divided into groups of ten; each group drew lots…, and the soldier on whom the lot fell was executed by his nine comrades, often by stoning or clubbing.” – Wikipedia[/ref] so it’s not a happy word, but it certainly doesn’t mean “to kill just about everyone.” Except that these days, it pretty much does, and you’ll get strange looks if you used it in any other way. How long before “enormity” goes on a similar list, and only out-of-touch cranks cling to its older definition and go on rants about ancient military laws?

It’s also worth pointing out that a lot of linguistic innovation is pretty fun and cool. For example: English Has a New Preposition, Because Internet.

But I draw the line at “steep learning curve” because we’re not just talking about illiteracy. We’re talking about innumeracy[ref]See? I’m down with neologisms[/ref].

A learning curve is a graph depicting the relationship between time (or effort) and ability. Time is the input: we put time into studying, practicing, and learning. And ability is the output: it’s what we get in return for our efforts. Generally we assume that there will be a positive relation between the two: the more you practice piano the better you’ll be able to play. The more you study your German vocabulary, the more words you will learn.

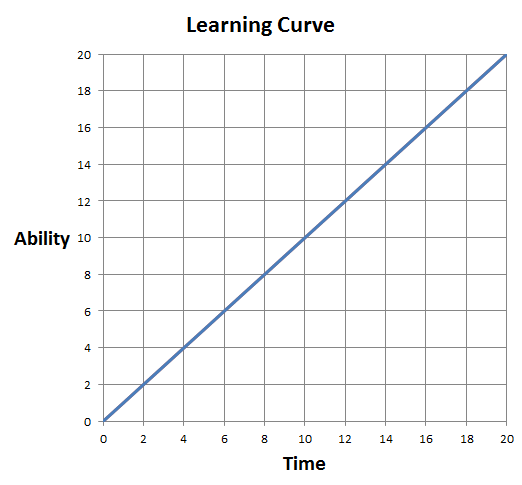
Basic Learning Curve

The graph right above this paragraph shows a completely ordinary, run-of-the-mill learning curve.[ref]Don’t worry that it’s actually a straight line. That’s just faster to make in Excel.[/ref] What units are we measuring ability and time in? Doesn’t matter. It would depend on the situation. Time would usually be measured in seconds or minutes or whatever, but in physical practice maybe you’d want to measure it in calories burned or some other metric. And ability would vary to: number of vocab words learned, percent of a song played without errors, etc. Now let’s take a look at two more learning curves:

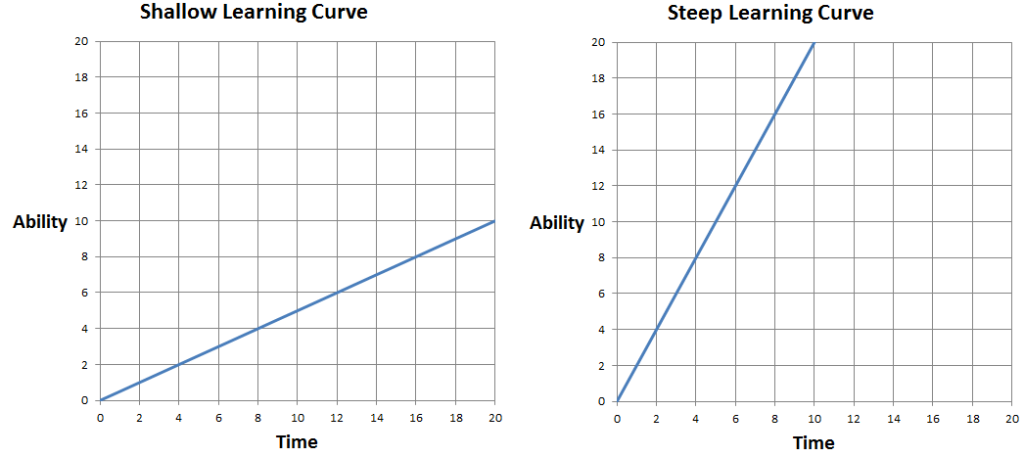
Learning Curve Comparison

The learning curve on the left is shallow. That means that for every unit of time you put into it, you get less back in terms of ability. The learning curve on the right is steep. That means that for every unit of time you put into it, you get more back in terms of ability. So here’s the simple question: if you wanted to learn something, would you prefer to have a shallow learning curve or a steep learning curve? Obviously, if you want more bang-for-the-buck, you want a steep learning curve. In this example, the steep learning curve gets you double the ability for half the time!

You might note, of course, that this is exactly the opposite of what Andrew Webster was trying to convey. He said that these kinds of games require “you to spend a lot of time getting killed before you understand how things actually work.” In other words: lots of time for little learning. In other words, he literally described a shallow learning curve and then called it steep. Earlier this morning my son tried to tell me that water is colder than ice, and that we make ice by cooking water. That’s about the level of wrongness in how most people use the term “steep learning curve.”

It’s not hard to see why people get confused on this one. We associate steepness with difficulty because it’s harder to walk up a steep incline than a shallow one. Say “steep” and people think you mean “difficult.” But visualizing a tiny person on a bicycle furiously peddling to get up the steep line on that graph is a fundamental misapprehension of what graphs represent and how they work. By convention, we put independent variables (that’s the stuff we can control, where such a category exists) on the x-axis  and dependent variables on the y-axis (that’s the response variable). Intuitions about working harder to climb graphs don’t make any sense.

Now, yes: it’s by convention that we organize the x- and y-axis that way. And conventions change, just like definitions of words change. And the convention isn’t always useful or applicable. So you could argue that folks who use the term “steep learning curve” are just flipping the axes. Right?

Wrong. First, I just don’t buy that folks who use the term have any such notion of what goes on which axis. They are relying on gut intuition, not graph transformations. Second, although the placement of data on charts is a convention, it’s not a convention that is changing. When people get steep learning curve wrong, they are usually not actually talking about charts or data at all, so they are just borrowing a technical term and getting it backwards. It’s not plausible to me that this single instance of getting the term backwards is actually going to cause scientists and analysts around the world to suddenly reverse their convention of which data goes where.

People getting technical concepts wrong is a special case of language where it does make sense to say that the usage is not just new or different, but is actually wrong. It is wrong in the sense that there’s a subpopulation of experts who are going to preserve the original meaning even if conventional speakers get it wrong and it’s wrong in the sense of being ignorant of the underlying rationale behind the term. Consider the idea of a quantum leap. This concept derives from quantum mechanics, and it refers to the fact that electrons inhabit discrete energy levels within atoms‘. This is–if you understand the physics at all–really very surprising. It means that when an electron changes its energy level it doesn’t move continuously along a gradient. It jumps pretty much directly from one state to the new state. This idea of “quanta“–of discrete quantities of time, distance, and energy–is actually at the heart of the term “quantum mechanics” and it’s revolutionary because, until then, physics was all about continuity, which is why it relied so heavily on calculus. If you use “quantum leap” to mean “a big change” you aren’t ushering in a new definition of a word the way that you are if you use “enormity” to mean “bigness”. In that case, once enough people get it wrong they start to be right. But in the case of quantum mechanics, you’re unlikely to reach that threshold (because the experts probably aren’t changing their usage) and in the meantime you’re busy sounding like a clueless nincompoop to anyone who is even passingly familiar with quantum mechanics. Similarly, if you say “steep learning curve” when you mean “shallow learning curve” then  you aren’t innovating some new terminology, you’re just being a dope.

Maybe it doesn’t matter, and maybe it’s even mean to get so worked up about technicalities. Then again, lots of people think the world would be a better place if people were more numerate, and I think there’s some truth to that. In any case, I’m a nerd and the definition of a nerd is a person who cares more about a subject than society thinks is reasonable.[ref]There’s a reason Cyrano de Begerac is my hero: “What? It’s useless? I know. A man doesn’t fight to win./It’s better when the fight is in vain.”[/ref]

Most importantly, however, if you get technical terms wrong you’re missing out. Because the term were chosen for a reason, and taking the time to learn that reason will always broaden your mind. One example, which I’ll probably write about soon, is the idea of a technological singularity. It’s a trendy buzzword you probably here futurists and sci-fi aficionados talking about all the time, but if you don’t know where the term originates (i.e. from black holes) then you won’t really understand the ideas that led to the creation of the term in the first place. And they are some pretty cool ideas.

So yeah: on the one hand this is just a rant from a crotchety old man telling the kids to get off his lawn.[ref]And turn down their music.[/ref] But my fundamental motivation is that I care about ideas and about sharing them with people. I rant with care. It’s a love-rant.

A History of Air Conditioning

by

Popular Mechanics has a fun timeline of air conditioning.  Given that it is the middle of summer and I live in Texas, I can’t imagine living without A/C. It is sometimes easy to forget that the first home-based air conditioning unit was installed for the first time 100 years ago “in the Minneapolis mansion of Charles Gates” and was “approximately 7 feet high, 6 feet wide, 20 feet long and possibly never used because no one ever lived in the house.” In 1970, only 36% of U.S. households had air conditioning. This percentage rose to 68% by 1993 and 87% by 2009 (this includes 81.6% of poor households). It also takes less energy in homes today, dropping to under 50% of U.S. home energy use. And to think no one before 1914 had one. 

So, enjoy your A/C along with an extra dose of gratitude.